Introduction

Quantum chromodynamic is the theory describing quarks, the fundamental building blocks of nature, and gluons, the particles "gluing" them together. This theory can be discretized and simulated in computational models, called lattice QCD. A typical lattice has 3 dimensions (interpreted as space-like) and one dimension (interpreted as time-like). Typically they are of the size of 16x16x16x32, which makes more than 130000 lattice sites.

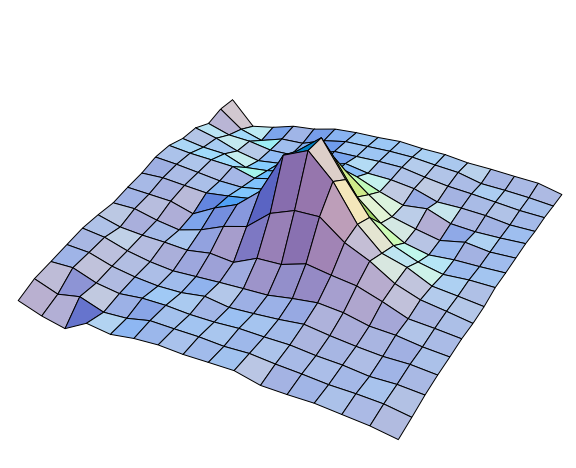
As starting configurations on such a lattice different gauge fields are needed; these are mathematical fields describing space time. Such gauge fields may have special topologies: next to big quantum fluctuations, that behave randomly, one can find classical solutions to the underlying equations. With different methods, such topologies are studied: smearing is one of them. It averages over whole loops in the lattice, in order to find the underlying topology.

This may be a bulp, as in the figure, that can be interpreted as an instanton, or a plane without instantons.

It is not absolutely clear in what way smearing changes the structure it wants to find. Therefore we tried to work with the raw data and search for different strucures.

Sonification approaches

• the data consists of real numbers on a regular, 4-dimensional lattice, with next-neighbor interactions and a torus-like structure
• there is random fluctuations and (in the chosen configurations) an underlying structure, a 4-d object typically of the size of 4x4x4x4

In the sonification, we started out with simple audification: the configuration was sequentialized by reading it either torus-like or following a Hilbert curve. The searched structures, instantons, are very short sound events in this approach. The relation between an instanton of e.g. 81 lattice sites vs. 130000 is just too small. Thus we made tools for sonifying a small region, a sub-hypercube, that were about the size of the instantons. This sonification can be interactively explored by moving 4 sliders (implemented for a GamePad with 2 sticks of each 2 axis and alternatively for 4 sliders of an audio mixer). It can also be automatically gone through, again taking the torus or Hilbert path.

For the sound mapping and in order to achieve some sort of non-linear amplification we experimented with resonators: in one approach, the sound signal of the audification of a sub-area was taken as input, and different frequencies (random, whole tones scale etc.) were used as resonators. In a different idea, the values of the sites were used as resonators and white noise was the input signal.