Introduction to spin models

Spin systems describe macroscopic properties of materials (e.g. ferro-magnetism, but even social systems have been simulated using e.g. the Ising model) by computational models of simple microscopic interactions between single elements of the material. The principal idea of modeling spin systems is to study a complex system in a controlled way, where they are theoretically tractable and mirror the behavior of real compounds. One of the oldest and best studied models are the Ising model, and one of its generalizations, the Potts model.

Spin models have been an interesting subject for studies for decades, and results in this field can be applied to many scientific domains. Most classical methods of solving them rely on mean values, whereas especially at the critical point of phase transition the fluctuations of single spins are their most important feature. We found that sound is an ideal display mode to study these fluctuations and the dynamic evolution of the whole model.

Our goal was to display three-dimensional dynamic systems, distinguish the different phases and study the order of the phase transition. Both real-time monitoring of the running model and analysis of pre-recorded data sets should be tested. Also analytic data pre-processing was done.

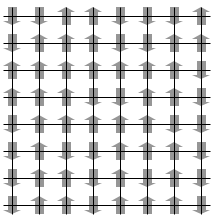
As shown in the figure it is assumed, that the magnet consists of simple atoms on a quadratic (or in three dimensions cubic) lattice. At each lattice point an "atom" is located with a magnetic moment (a spin) up or down. In the computation, on the one hand, neighboring spins try to align to each other, which is energetically more favorable. On the other hand, an overall temperature causes random spin flips. At a critical temperature, this process is undecided and there are clusters of spins on all orders of magnitude. If the temperature is lowered from T_crit, one spin orientation will prevail. (Which one is decided by the random initial setting.) Macroscopically, this is the magnetic phase (TT_crit, the thermal fluctuations are too strong for uniform clusterings of spins. There is no macroscopic magnetization, only thermal noise.

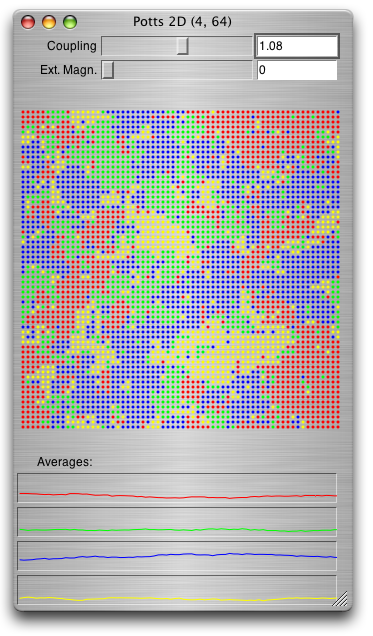
Spin models are nowadays usually simulated with Monte-Carlo algorithms. We implemented a Monte Carlo simulation for an Ising and Potts model in SuperCollider3. The lattice is represented as a torus and continually updated: for each lattice point, a different spin state is proposed, and the new overall energy calculated. It depends on the neighbor's interactions and the overall temperature. If the new energy is smaller than the old one, the new state is accepted. If not, there is still certain chance that it is accepted, leading to random spin flips representing the overall temperature.

Sonifications

• Granular Sonifications

  In this approach, the data was pre-processed. Thus, the sound can be better controlled and is more convenient to listen to than an audification based approach.

  In a cloud sonification we tried to sonify each spin as a very short soundgrain, and played them slightly delayed within a short time frame. For a 32x32 lattice this is doable in one second, which leaves about 3 ms for each sound grain. One second is not as fast as one would like to go through the entire frame, but a trade-off with the fact that we still play all available information. For bigger lattices, this approach is too slow for practical use.

  Thus a similar approach was calculating mean values beforehand. We took random averaged spin blocks in the Ising model.

• Audification Based Sonification

  In this approach, we tried to utilize all possible information of the model. The basic idea was an audification, where the spins determine a waveform. The resulting sound wave can be listened to directly or taken as a modulator of a sine wave. When the temperature is lowered, regular clusters emerge, changing only slowly from time step to time step. Thus also in the audification longer structures will emerge, resulting in more tone-like sounds. When one spin dominates, there is no sound (except of some random thermal fluctuations at non-zero temperature).

  We tried out two different ways to sequentialize the lattice: either we went by the normal torus path or by a Hilbert-curve (a space filling curve for quadratic spaces).

• Channel Sonification

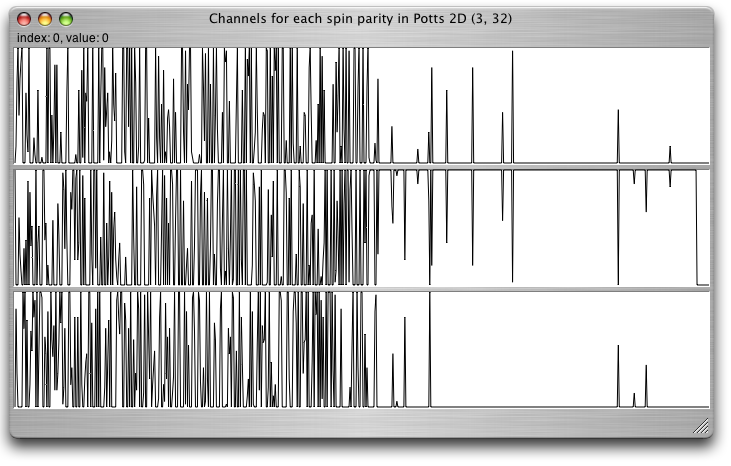
  Finally we refined the audification approach, and allowed to record data for each spin separately. Here, the different spins can be separated, e.g. in their basic frequency when using the audio wave for a modulation. This design already gives very interesting results for the direct playback of the buffers.

Conclusion

A number of different sonifications were designed in order to study different aspects of spin models. We created a tool for the perceptualization of lattice calculations, extendable to higher dimensions and a higher number of states. On the one hand, running models can be observed. On the other hand, pre-recorded data can be analyzed in a way to get a first impression of the order of the phase transition.